Funciones de regresión: Cálculo de la pendiente.
En el presente artículo, vamos a tratar de aclarar para todos nuestros usuarios la diferencia existente entre dos funciones que, de inicio, pueden parecer lo mismo.
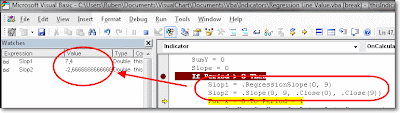
a) pendiente = RegressionSlope(0,9)
b) pendiente = Slope(0,9,.Close(0),.Close(9))
Si embargo, al aplicar dichas funciones, observamos que cada una devuelve resultados distintos:
Por tanto, la pregunta que nos surge es la siguiente: ¿Qué diferencias existen entre utilizar una función u otra?¿Cuál nos interesaría utilizar para nuestro propósito? Vamos a tratar de dar respuesta a estas preguntas.
La función SLOPE
La función Slope nos devuelve la función de PENDIENTE clásica, calculada entre dos vectores a1 y a2 en los que cada uno de estos vectores tienen sus coordenadas cartesianas (x,y). En nuestro caso, el eje de abscisas estaría representado por el TIEMPO o NUMERO DE BARRAS, mientras que el eje de ordenadas estaría representado por los precios.
La función utilizada viene a ser la siguiente:
Slope = (EndPrice - StartPrice) / (EndBar - StartBar)
Obteniendo el siguiente resultado:
La función REGRESSIONSLOPE
La función RegressionSlope nos devuelve el valor de la pendiente de la ecuación de regresión. Esta ecuación varía sensiblemente respecto a la función vista anteriormente, ya que en este caso lo que hace es calcular la recta de regresión entre el cierre de la barra inicio y el cierre de la barra fin y posteriormente calcula la pendiente de dicha recta.
La función utilizada viene a ser la siguiente:
for(int i = StartBar; i < EndBar; i++)
{
//Obtener x, y
x = i;
y = CIERRE(x);
//Calcular datos
nEx += x;
nEy += y;
nExy += (x * y);
nEx2 += (x * x);
}
// Calcular la pendiente a partir de los datos
// n • Sum(x • y) - Sum(x) • Sum(y)
// m = -------------------------------
// n • Sum(x^2) - Sum(x)^2
double nNum = EndBar - StartBar;
double nDenom = nNum * nEx2 - nEx * nEx;
if(nDenom != 0)
RegSlope = (nNum * nExy - nEx * nEy) / nDenom;
else
RegSlope = 0.0;
Obteniendo el siguiente resultado:
Por tanto, para dar solución al ejemplo que hemos planteado al inicio del artículo, usaríamos la función RegressionSlope especificando lo siguiente:
pendiente = RegressionSlope(Bar-9, Bar)




Comentarios
Publicar un comentario